programmierung
und datenbanken
Joern Ploennigs
Algorithmen
Ablauf¶
Algorithmen¶
Algorithmen sind wohldefinierte, eindeutige Handlungsanweisungen.
- Bekannte Beispiele:
- Schriftliche Division
- Dreieckskonstruktion
- In der Informatik-Praxis: computerausführbar und endlich
- Programmieren bedeutet Algorithmen und Datenstrukturen so zu kombinieren, dass man von der gewünschten Eingabe zur gewünschten Ausgabe kommt.
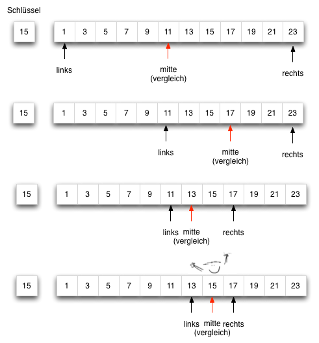
Beispiel für Teile und Herrsche – Binäre Suche¶
Finde den Index einer Zahl in einer Liste (z. B. um zu prüfen ob die Zahl in einer Menge (set) vorkommt)
Anstatt die ganze Liste zu durchsuchen, teil man die Liste rekursiv in zwei Teile und schaut ob die gesuchte Zahl gleich (gefunden), größer (rechts) oder kleiner (links) in der Liste ist
Heuristiken¶
Basieren nicht auf wohldefinierten oder eindeutigen Schritten, sondern auf praktischen Erfahrungen
Versuchen schnell ein hinreichend korrektes Ergebnis zu erreichen. KEINE Garantie die optimale Lösung zu finden.
Beispiel:
- Die Schätzung eines Experten
- Schrittweises Annähern
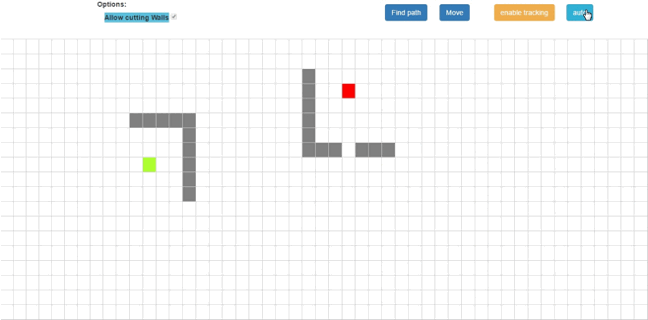
Exkurs – Beispiel für eine Heuristik: A*Star Suchalgorithmus¶
Die Wegsuche gehört zu den komplexesten Problemen in der Informatik (NP-Komplex: Aufgrund des kombinatorischen Problems)
A* ist eine Heuristik um den kürzesten Weg zwischen zwei Punkten in einem Feld mit Hindernissen zu finden
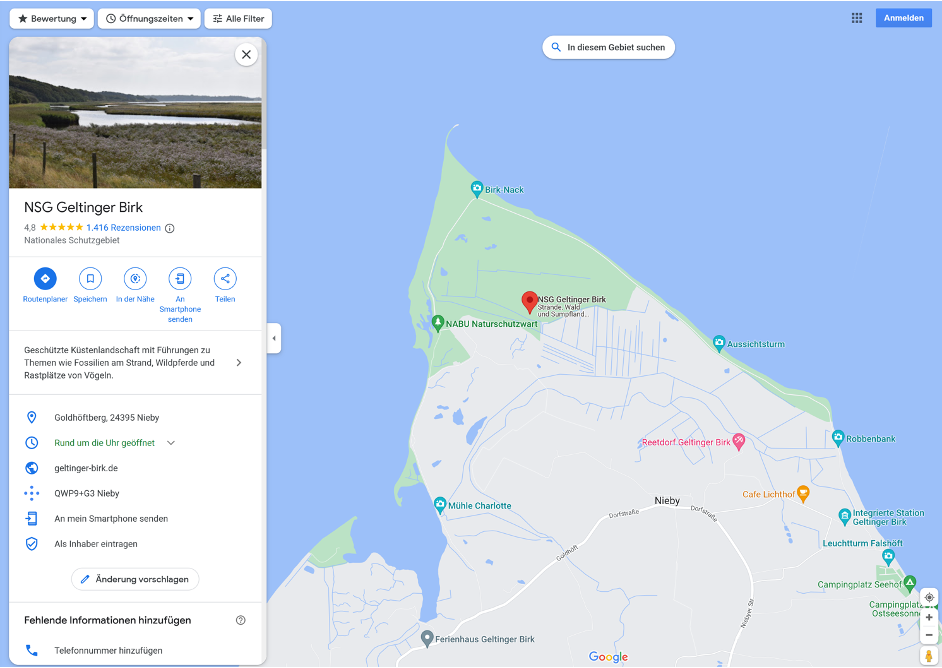
Beispielproblem - Befindet sich ein Punkt X in einem Polygon?¶
Ein Polygon ist ein beliebiges Vieleck
Die Lösung dieses Problems ist ein häufiger Teil von Berechnungen in den Bau- und Umweltwissenschaften, z. B. um zu testen, ob ein geplantes Objekt in einem Naturschutzgebiet liegt.
Hörsaalfrage¶
Wie kann ich bestimmen ob ein Punkt in einem Polygon liegt?
Beispielproblem - Was sind unsere Aus- und Eingaben?¶
Eingaben:
- Die Position des Punktes
x - Ein Linienzug der den Rand des Polygons beschreibt
- Eine Liste von verbundenen, aufeinanderfolgenden Linien
Ausgaben:
Ein Boolean
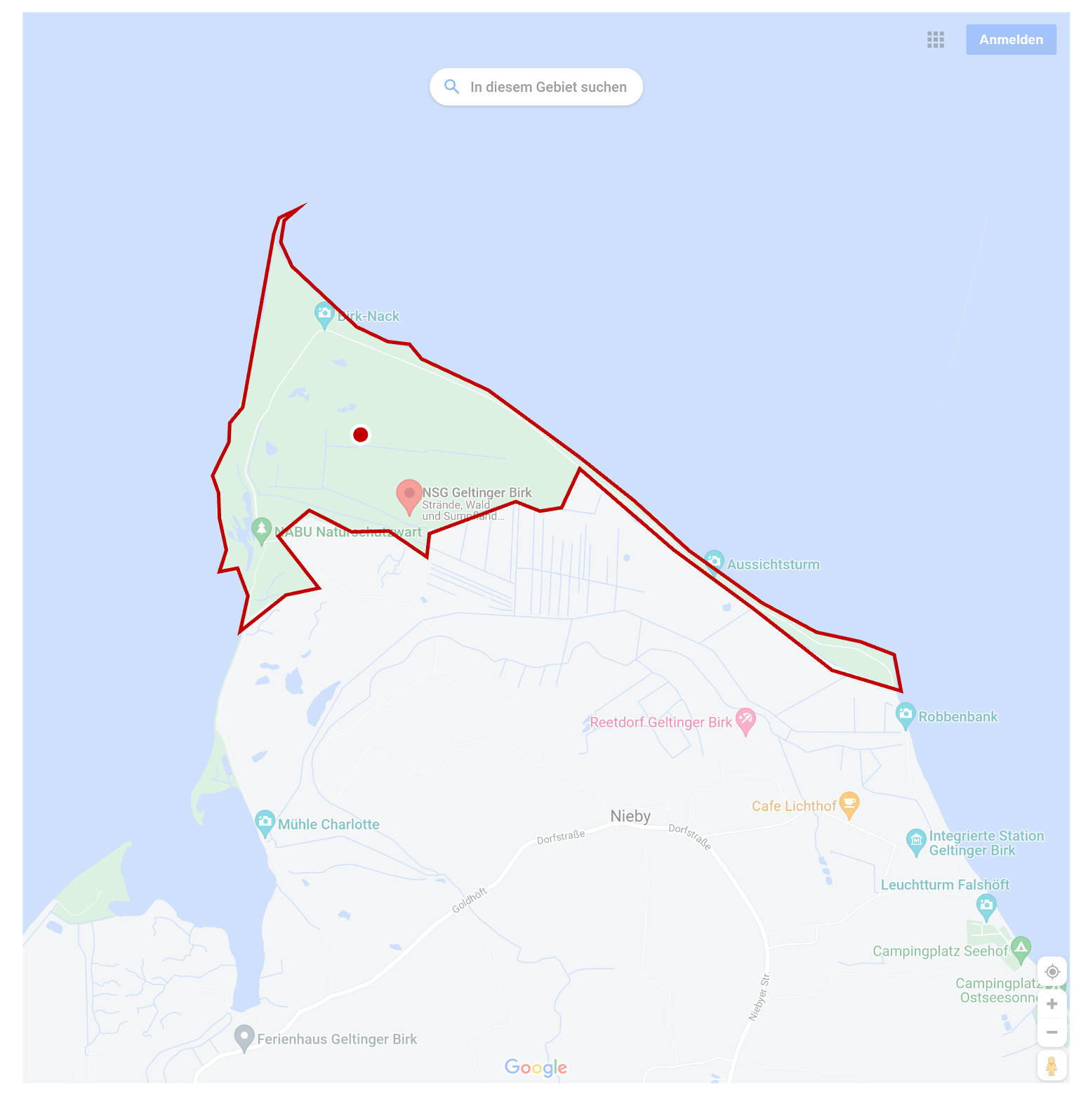
Beispielproblem - Entwerfen eines Algorithmus¶
Was sind Berechnungen, die man auf Punkten und Linien ausführen kann?
Wir können prüfen ob der Punkt genau auf einer Linie liegt.
Wir können prüfen auf welcher Seite einer Linie ein Punkt liegt.
Reicht Punkt 2 aus? Für konvexe Flächen - ja, befindet sich der Punkt auf der gleichen Seite aller Linien des Polygons, befindet er sich im Polygon.
Trifft aber nicht für konkave Flächen zu => es handelt sich also um eine Heuristik!
Beispielproblem - Entwerfen eines Algorithmus¶
Entwurf bedeutet oft ein Problem aus verschiedenen Richtungen zu betrachten und neue Berechnungsperspektiven zu finden.
Hier: Die Krux ist ob eine Fläche konkav oder konvex ist. Man bestimmt diese Eigenschaften durch das Ziehen von Linien und Schnitttests.
Liegt der Schlüssel zu diesem Problem also in den Schnitttests zwischen Linien?
Gibt es eine Linie vom gesuchten Punkt
Xzu einem anderen PunktY, deren Schnittpunkte mit den Polygon-Linien eine Antwort auf die Fragestellung geben?
Beispielproblem - Entwerfen eines Algorithmus¶
Die Antwort: Jeder beliebige Punkt außerhalb des Polygons!
Liegt Punkt
Xinnerhalb des Polygons dann wird die gezogene Linie die Grenze mindestens einmal schneiden.Läuft die gezogene Linie zufällig durch einen konkaven Bereich dann wird es zwei weitere Schnittpunkte geben, für insgesamt 3 Schnittpunkte, oder 5, oder …
Liegt der Punkt
Xaußerhalb wird es also entweder keine Schnittpunkte geben, oder 2, oder 4, oder …Das Problem kann also auf die Anzahl von Schnittpunkten reduziert werden!
Beispielproblem - Beispiel¶
Beispielproblem - Als Programmablaufplan aufzeichnen¶
Beispiele für:
- Strahl 1 hat 1 Schnittpunkt → ungerade = innenliegend
- Strahl 2 hat 3 Schnittpunkte → ungerade = innenliegend
- Strahl 3 hat 5 Schnittpunkte → ungerade = innenliegend
Rekursion - Beispiel: Tree Traversal¶
Baum: Datenstruktur, in der jedes Element auf weitere Unterelemente verweisen kann.
Nun wollen wir eine Funktion auf jedes Element im Baum anwenden.
Simpelste Repräsentation eines Baumes:
- Ein Tupel mit einem Wert und einer Liste
- Diese Liste enthält Tupel mit jeweils einem Wert und einer Liste (Rekursive Datenstruktur!)
12
/ \
6 18
/ \ / \
3 9 15 21
baum = (12, [
(6,[
(3,[]),
(9,[])
]),
(18,[
(15,[]),
(21,[])
])
])
Rekursion - Beispiel: Tree Traversal¶
Traversals sind Funktionen welche den Baum durchlaufen, z.B. um Elemente zu suchen.
Informatik-Exkurs: Sortieren¶
- Speziell das Sortieren von Listen, unabhängig vom Datentyp
- Eine der Standard-Anwendungen für Schleifen und Rekursion
- Die Lösung im Programmieralltag:
sorted() - Aber: Gutes Beispiel für strukturiertes Informatik-Problem
Sortieren - Algorithmus 1: Bubble Sort¶
- Jedes Element der Liste wird durchlaufen und mit dem nächsten Element verglichen.
- Ist das zweite Element kleiner als das erste wird die Position getauscht.
- Die Liste wird immer wieder durchlaufen bis dieser Fall nicht mehr auftritt.
def bubbleSort(numbers):
for i in range(len(numbers)-1):
for j in range(0, len(numbers)-i-1):
if numbers[j] > numbers[j + 1]:
numbers[j], numbers[j + 1] = numbers[j + 1], numbers[j]
Sortieren - Algorithmus 2: Quick Sort¶
Das Grundprinzip ist das Aufteilen der Liste:
- Das erste Element der Liste als „Pivot"-Element abspeichern.
- Dann wird die Liste durchlaufen und jedes Element mit dem Pivot verglichen.
- Einsortiert in eine von drei Listen: Kleiner, Gleich und Größer.
- Dann wird Quick Sort rekursiv auf die Listen Kleiner und Größer ausgeführt.
- Am Ende werden alle Listen rekursiv wieder zusammengeführt.
Informatik-Exkurs: Suchen¶
- Speziell das Suchen auf sortierten Listen und Bäumen
- Meist kennt man die Anzahl an Elementen, weiß also genau wo z.B. die Mitte ist.
- Spätere Vorlesungen: In echten Anwendungen haben Datensätze oft mehr als nur einen Wert (Tabellen anstatt Listen), hier arbeitet man meist mit Indexierung.
Suchen - Suche in Listen¶
Die einfachste Methode: lineare Suche
def contains(list, x):
for l in list:
if(l == x):
return True
return False
Suchen - Suche in Listen¶
Das optimale Verfahren: Binäre Suche
- Deutlich komplexerer Code
- Idee: Mittleres Element der Liste finden, dann mit dem gesuchten Wert vergleichen
- Wert kleiner: Selbes Verfahren für die erste Hälfte der Liste
- Wert größer: Selbes Verfahren für die zweite Hälfte der Liste
- Implementation meistens über Rekursion
Suchen - Suchen in Bäumen¶
Strategien um einen unsortierten Baum zu durchsuchen:
- Breitensuche: Vom Ursprung beginnend jede „Ebene" des Baumes von links nach rechts durchlaufen.
- Tiefensuche: Einem Pfad vom Ursprung bis zum Ende folgen, dann schrittweise rückwärts gehen bis sich weitere Pfade anbieten.
Suchen - Suchen in Bäumen¶
In sortierten Bäumen (Suchbäumen) kann das Ergebnis extrem effizient gefunden werden, da nur ein Pfad durchlaufen werden muss.
Wie sortiert man einen Baum?
Erstellen eines binären Suchbaums¶
Ausgangsliste: 12 6 18 15 3 21 9
Schritt 1: 12 als Wurzel setzen
12
Schritt 3: 18 > 12, rechts einfügen
12
/ \
6 18
Schritt 2: 6 < 12, links einfügen
12
/
6
Schritt 4: 15 > 12, aber 15 < 18
12
/ \
6 18
/
15
Suchbaum - Fortsetzung¶
Schritt 5: 3 < 12 und 3 < 6
12
/ \
6 18
/ /
3 15
Schritt 7: 9 < 12 aber 9 > 6
12
/ \
6 18
/ \ / \
3 9 15 21
Schritt 6: 21 > 12 und 21 > 18
12
/ \
6 18
/ / \
3 15 21
Fertiger Suchbaum!
Exkurs: Komplexität und effiziente Algorithmen¶
Die eigentliche Berechnungszeit ergibt sich erst durch die genauen Eingabedaten und den genutzten Prozessor.
Formal ist Effizienz stattdessen eher eine Anstiegskurve, welche eine relative Schätzung abgibt wie viel länger ein Algorithmus bei mehr Eingabedaten rechnen muss.
Notation: $O(x)$, wobei $x$ die Menge der nötigen Rechenschritte angibt.
Für Bäume und Listen hängt diese von der Anzahl an Elementen ab (Variable $n$).
Komplexität - Vergleich der Algorithmen¶
Suchverfahren:
Lineare Suche $$O(n)$$
Binäre Suche $$O(log(n))$$
Sortierverfahren:
Bubble Sort $$O(n^2)$$
Quick Sort $$O(n \cdot log(n))$$
fragen?
und datenbanken