Programming
and databases
Joern Ploennigs
Algorithms
Process¶
Algorithms¶
Algorithms are well-defined, unambiguous instructions.
- Known examples:
- Long division
- Triangle construction
- In computer science practice: computer-executable and terminating
- Programming means combining algorithms and data structures in such a way that you obtain the desired input to the desired output.
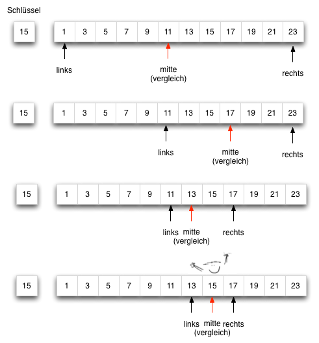
Example for Divide and Conquer – Binary Search¶
Find the index of a number in a list (e.g., to check whether the number occurs in a set)
Instead of searching the entire list, you split the list recursively into two parts and check whether the searched number is equal (found), greater (to the right), or smaller (to the left) in the list
Heuristics¶
They are not based on well-defined or unambiguous steps, but on practical experience
They aim to quickly achieve a sufficiently accurate result. There is no guarantee to find the optimal solution.
Example:
- An expert's estimate
- Stepwise approximation
Excursus – Example of a heuristic: the A* search algorithm¶
Pathfinding is one of the most complex problems in computer science (NP-complete: due to the combinatorial nature of the problem)
A* is a heuristic for finding the shortest path between two points in a grid with obstacles
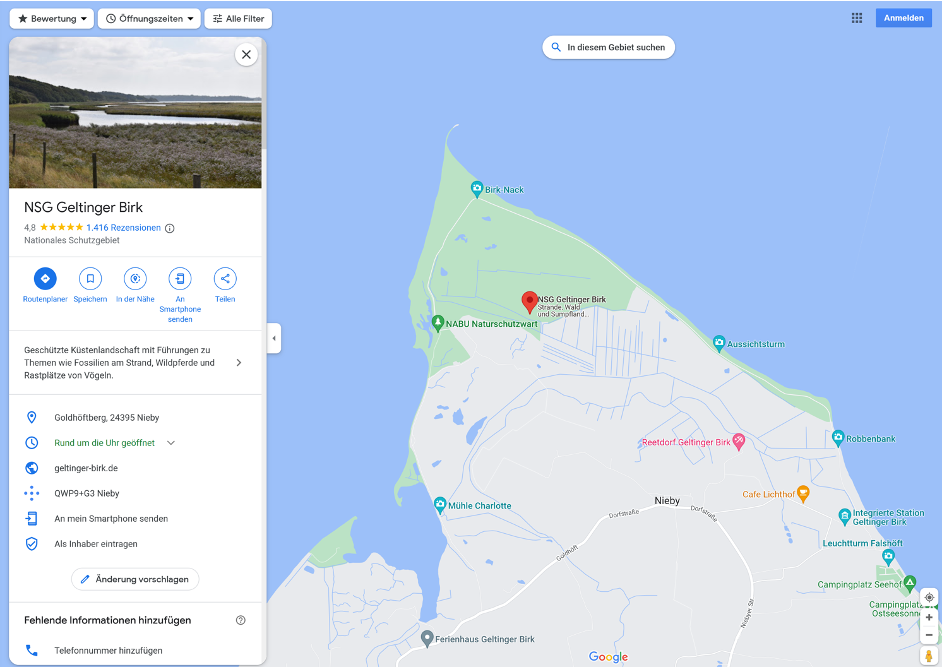
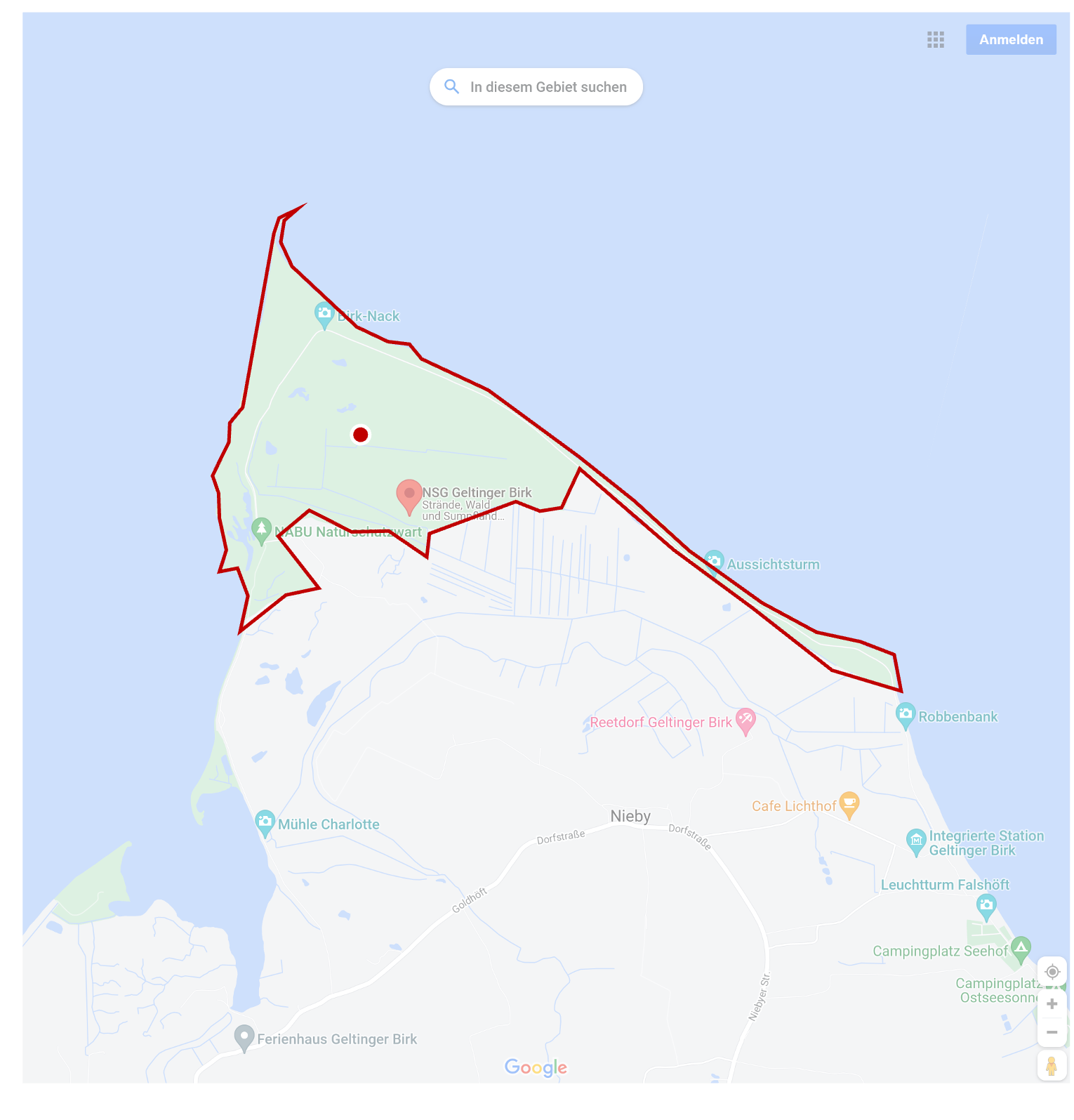
Example problem - Is a point X inside a polygon?¶
A polygon is an arbitrary polygon
The solution to this problem is a common part of calculations in civil engineering and environmental sciences, e.g., to test whether a proposed project lies within a nature reserve.
Lecture Hall Question¶
How can I determine whether a point lies inside a polygon?
Example problem - What are our inputs and outputs?¶
Inputs:
- The position of the point
x - A polyline describing the boundary of the polygon
- A list of connected, consecutive lines
Outputs:
A Boolean
Example problem - Designing an algorithm¶
What computations can be performed on points and lines?
We can check whether a point lies exactly on a line.
We can check on which side of a line a point lies.
Is Point 2 sufficient? For convex shapes – yes; if the point lies on the same side of all lines of the polygon, it lies inside the polygon.
But this does not hold for concave shapes => it is thus a heuristic!
Example Problem - Designing an Algorithm¶
Designing often means looking at a problem from different angles and finding new computational perspectives.
Here: The crux is whether a region is concave or convex. One determines these properties by drawing lines and performing intersection tests.
Is the key to this problem therefore in the intersection tests between lines?
Is there a line from the point in question
Xto another pointY, whose intersections with the polygon's edges provide an answer to the question?
Example Problem - Designing an Algorithm¶
The answer: Any point outside the polygon!
If the point
Xlies inside the polygon, the drawn line will intersect the boundary at least once.If the drawn line passes randomly through a concave region, there will be two more intersection points, for a total of 3 intersection points, or 5, or …
If the point
Xlies outside, there will thus be either no intersection points, or 2, or 4, or …Thus the problem can be reduced to the number of intersection points!
Example problem – example¶
Example problem - Draw as a program flowchart¶
Examples for:
- Ray 1 has 1 intersection point → odd = inside
- Ray 2 has 3 intersection points → odd = inside
- Ray 3 has 5 intersection points → odd = inside
Recursion - Example: Tree Traversal¶
Tree: A data structure in which each element can refer to further subelements.
Now we want to apply a function to every element in the tree.
Simplest representation of a tree:
- A tuple with a value and a list
- This list contains tuples, each with a value and a list (a recursive data structure!)
12
/ \
6 18
/ \ / \
3 9 15 21
baum = (12, [
(6,[
(3,[]),
(9,[])
]),
(18,[
(15,[]),
(21,[])
])
])
Recursion - Example: Tree Traversal¶
Traversals are functions that traverse the tree, e.g., to search for elements.
CS Aside: Sorting¶
- Specifically the sorting of lists, regardless of data type
- One of the standard use cases for loops and recursion
- The go-to solution in everyday programming:
sorted() - But: a good example of a structured computer science problem
Sorting - Algorithm 1: Bubble Sort¶
- Each element in the list is traversed and compared with the next element.
- If the next element is smaller than the current one, swap their positions.
- The list is repeatedly traversed until no swaps occur.
def bubbleSort(numbers):
for i in range(len(numbers)-1):
for j in range(0, len(numbers)-i-1):
if numbers[j] > numbers[j + 1]:
numbers[j], numbers[j + 1] = numbers[j + 1], numbers[j]
Sorting - Algorithm 2: Quick Sort¶
The basic principle is partitioning the list:
- Store the first element of the list as the pivot element.
- Then traverse the list and compare each element with the pivot.
- Insert into one of three lists: Smaller, Equal, and Greater.
- Then Quick Sort is applied recursively to the Smaller and Greater lists.
- In the end, all the lists are recursively merged back together.
Computer Science Digression: Searching¶
- Specifically searching on sorted lists and trees
- Most of the time you know the number of elements, so you know exactly where the middle is, for example.
- Later lectures: In real-world applications, datasets often have more than one value (tables instead of lists); here one typically works with indexing.
Searches - Searching in Lists¶
The simplest method: linear search
def contains(list, x):
for l in list:
if(l == x):
return True
return False
Searching - Searching in Lists¶
The optimal method: Binary search
- Significantly more complex code
- Idea: Find the middle element of the list, then compare it with the target value
- If the value is smaller: use the same procedure for the first half of the list
- If the value is larger: use the same procedure for the second half of the list
- The implementation is usually via recursion
Search - Searching in Trees¶
Strategies for searching an unordered tree:
- Breadth-first search: Beginning at the root, traverse each level of the tree from left to right.
- Depth-first search: Follow a path from the root to the end, then backtrack step by step until more paths become available.
Searching - Searching in Trees¶
In sorted trees (search trees), the result can be found extremely efficiently, since only a single path needs to be traversed.
How do you sort a tree?
Creating a Binary Search Tree¶
Initial list: 12 6 18 15 3 21 9
Step 1: Set 12 as the root
12
Step 3: 18 > 12, insert on the right
12
/ \
6 18
Step 2: 6 < 12, insert on the left
12
/
6
Step 4: 15 > 12, but 15 < 18
12
/ \
6 18
/
15
Search Tree - Continuation¶
Step 5: 3 < 12 and 3 < 6
12
/ \
6 18
/ /
3 15
Step 7: 9 < 12 but 9 > 6
12
/ \
6 18
/ \ / \
3 9 15 21
Step 6: 21 > 12 and 21 > 18
12
/ \
6 18
/ / \
3 15 21
Finished search tree!
As an aside: Complexity and Efficient Algorithms¶
The actual computation time is determined only by the exact input data and the processor used.
Formally, efficiency is better described as an increasing curve that provides a relative estimate of how much longer an algorithm must run as the input data grows.
Notation: $O(x)$, where $x$ denotes the amount of necessary computation steps.
For trees and lists, this depends on the number of elements (variable $n$).
Complexity - Comparison of Algorithms¶
Search algorithms:
Linear search $$O(n)$$
Binary search $$O(log(n))$$
Sorting algorithms:
Bubble Sort $$O(n^2)$$
Quick Sort $$O(n \cdot log(n))$$
Questions?
und datenbanken